ANALISIS DE LA SEGUNDA DERIVADA

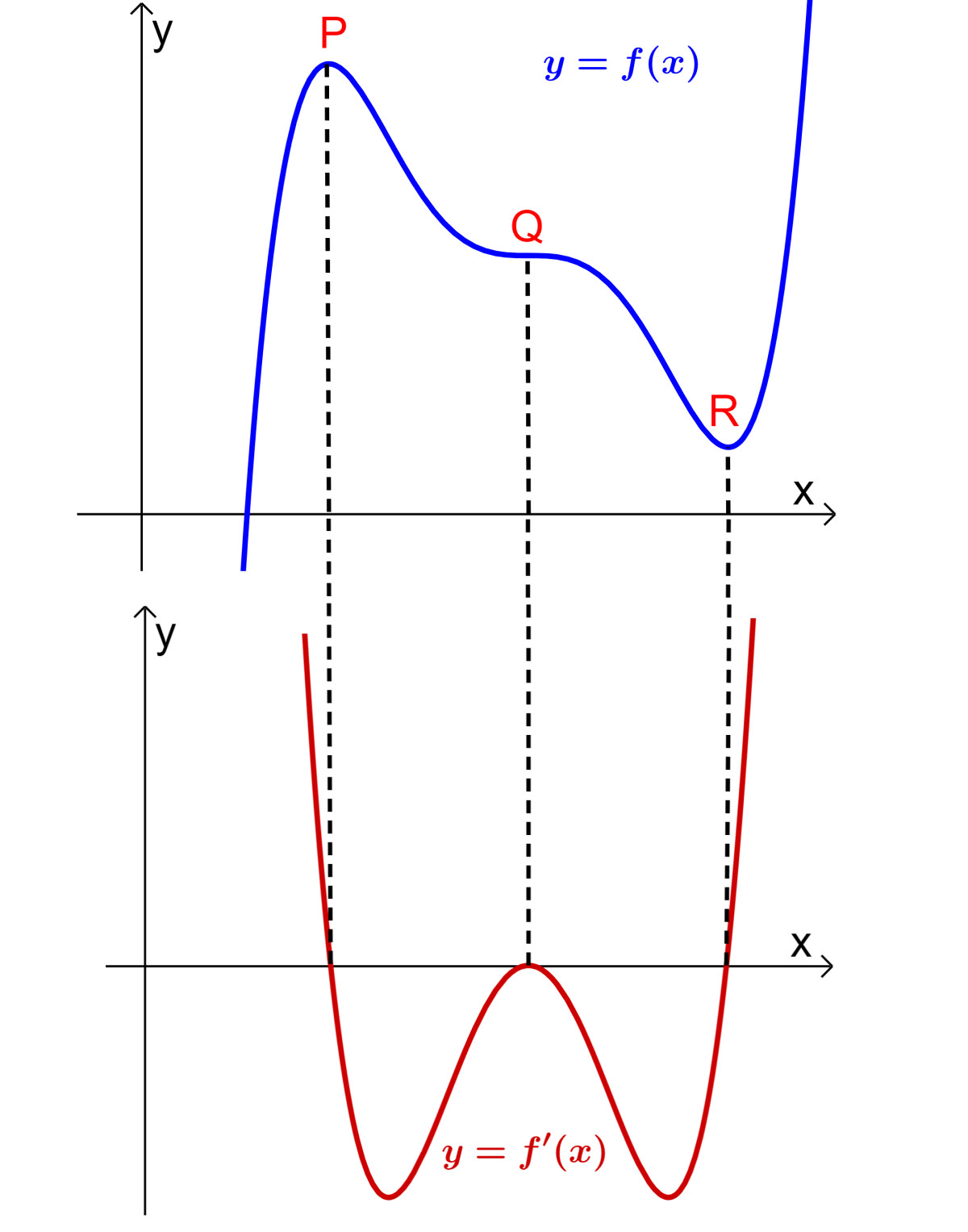
El análisis de la segunda derivada es una herramienta fundamental en el cálculo que se utiliza para determinar la concavidad de una función y para identificar los máximos y mínimos locales. A continuación, se presentan los aspectos clave de este análisis.

La segunda derivada de una función f(x), denotada como f′′(x), es la derivada de la derivada def(x). Esto significa que se obtiene al derivar la función derivada f′(x). La segunda derivada proporciona información sobre cómo cambia la pendiente de la función original, es decir, describe la aceleración de la función. 

Gráficamente, la segunda derivada ayuda a identificar los puntos de inflexión, que son puntos donde la concavidad de la función cambia. En estos puntos, la segunda derivada cambia de signo, lo que indica que la función pasa de ser cóncava hacia arriba a cóncava hacia abajo, o viceversa.

El análisis de la segunda derivada es ampliamente utilizado en diversas áreas, como la economía, la física y la ingeniería, para optimizar funciones y modelar fenómenos. Por ejemplo, en economía, se puede utilizar para determinar el nivel de producción que maximiza las ganancias o minimiza los costos. 

FUNCIÓN CÓNCAVA

Ejercicio 1: Función (Cóncava hacia Arriba)

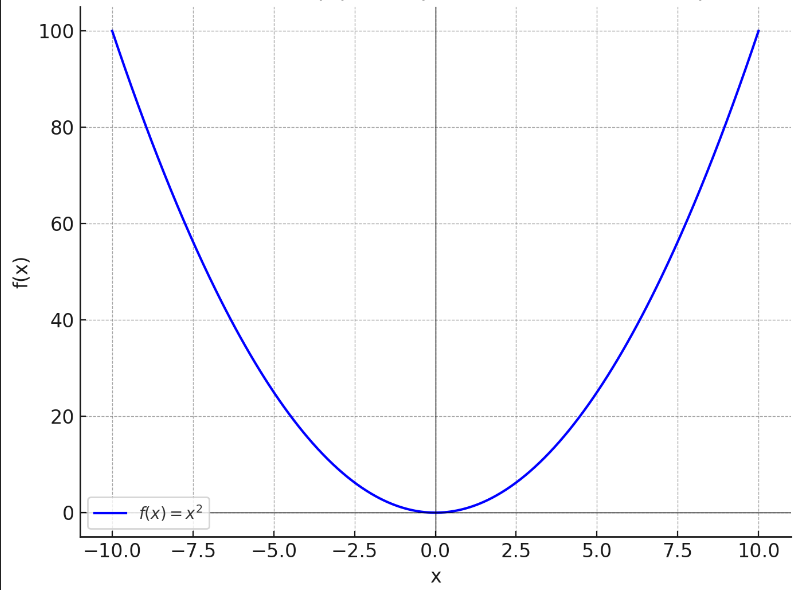
Dada la función f(x) = x^2, determinar si es cóncava hacia arriba.

Solución:

1. Calcula la segunda derivada de la función:

   La función es f(x) = x^2

   Su primera derivada es:

   f′(x)=2x

   La segunda derivada es:

   f′′(x)=2

2. Determina el signo de la segunda derivada:

   En este caso, f′′(x)=2, que es positivo para todo x.

Conclusión:

Como la segunda derivada es positiva en todo el dominio de f(x)f(x)f(x), la función f(x) = x^2 es cóncava hacia arriba en todo el intervalo real (−∞,∞).

FUNCIÓN CÓNCAVA 

Ejercicio 2: Función Cóncava (Cóncava hacia Abajo)

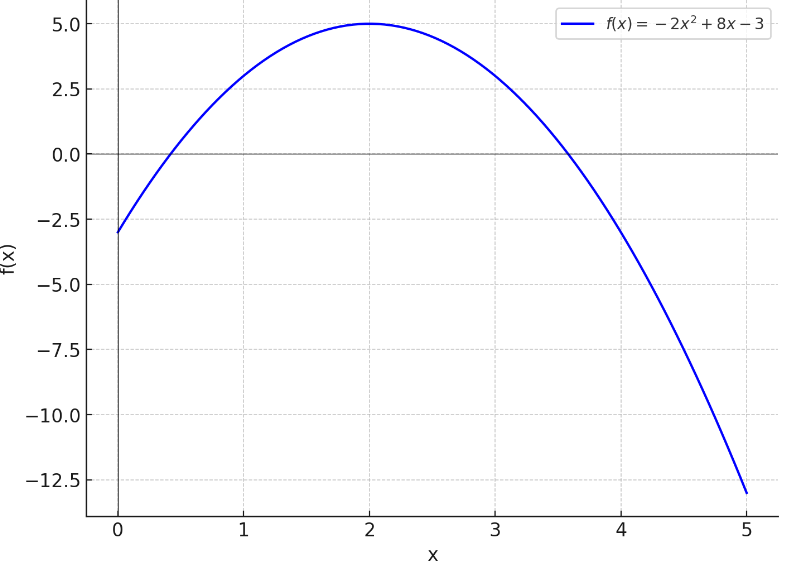
Dada una función f(x) = -2x^2 + 8x - 3, demuestra que es cóncava hacia abajo.

Solución:

1. Calcula la primera derivada f′(x):

   f'(x) = -4x + 8

2. Calcula la segunda derivada f′′(x):

3. f''(x) = -4

4. Observa que f''(x) = -4 < 0, lo que indica que f(x) es cóncava hacia abajo en todo su dominio.

CONCLUSIÓN

La gráfica también muestra que esta función alcanza un máximo en su vértice, lo cual es característico de las funciones cóncavas hacia abajo. En este caso, ese máximo ocurre en el punto x=2, con el valor máximo de f(x)=5.

Este ejercicio ilustra cómo identificar y analizar funciones cóncavas hacia abajo, especialmente aquellas con una estructura cuadrática que presentan un máximo en su gráfica.

RESUMEN

El análisis de la segunda derivada permite determinar la concavidad de una función y encontrar sus máximos y mínimos locales. Si la segunda derivada f′′(x) es positiva en un intervalo, la función es cóncava hacia arriba (forma de "valle") en ese intervalo. Si f′′(x) es negativa, la función es cóncava hacia abajo.